Below is a simple example with two CT values (CT0, CT1) and one priority 0 as shown in Figure 1.
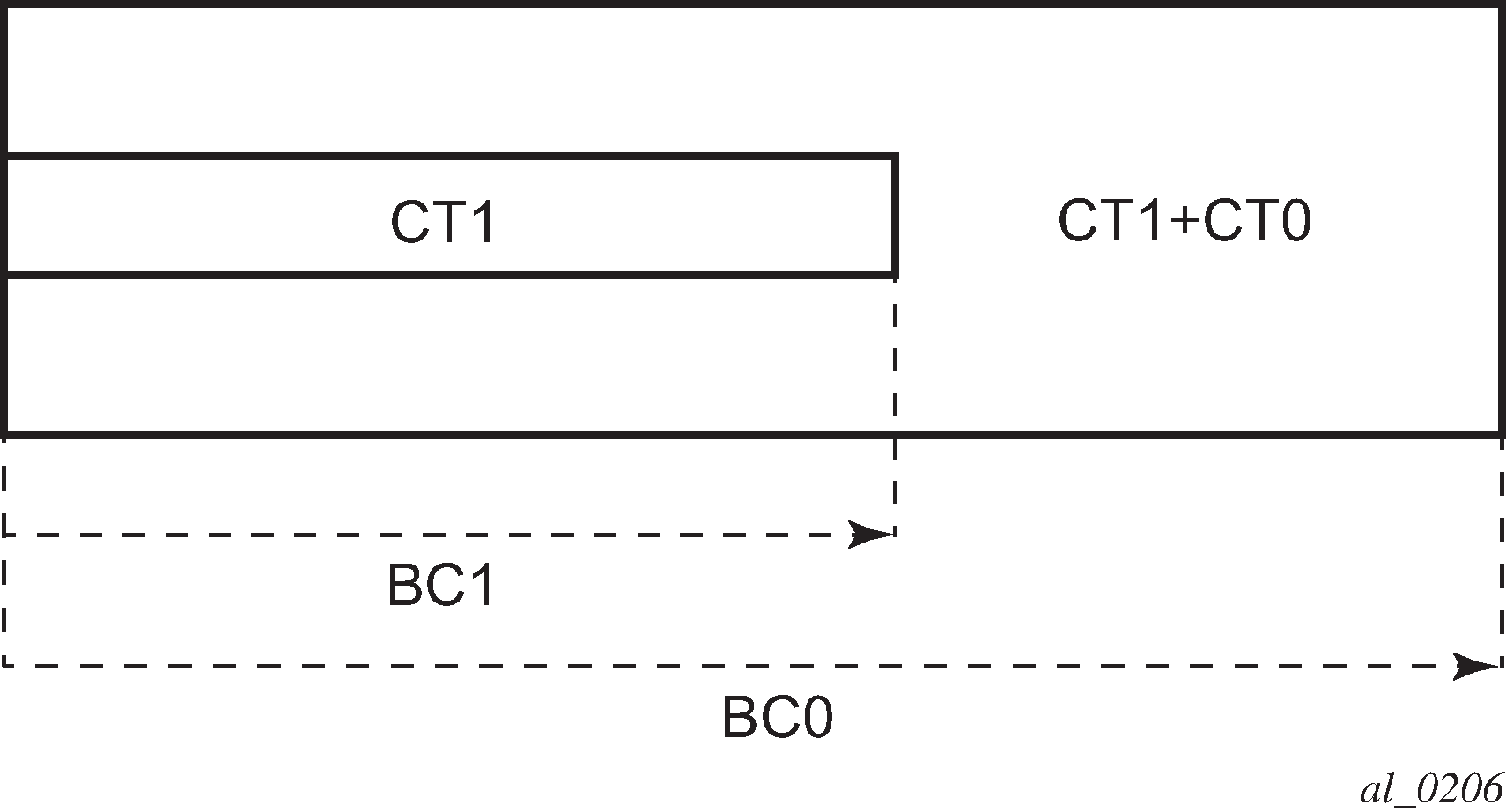
Suppose CT1 bandwidth, or the CT1 percentage of Maximum Reservable Bandwidth to be more accurate is 100 Mb/s and CT2 bandwidth is 100 Mb/s and link bandwidth is 200 Mb/s. BC constraints can be calculated as follows.
BC1 = CT1 Bandwidth = 100 Mb/s.
BC0 = {CT1 Bandwidth} + {CT0 Bandwidth} = 200 Mb/s.
Suppose an LSP comes with CT1, setup and holding priorities of 0 and a bandwidth of 50 Mb/s.
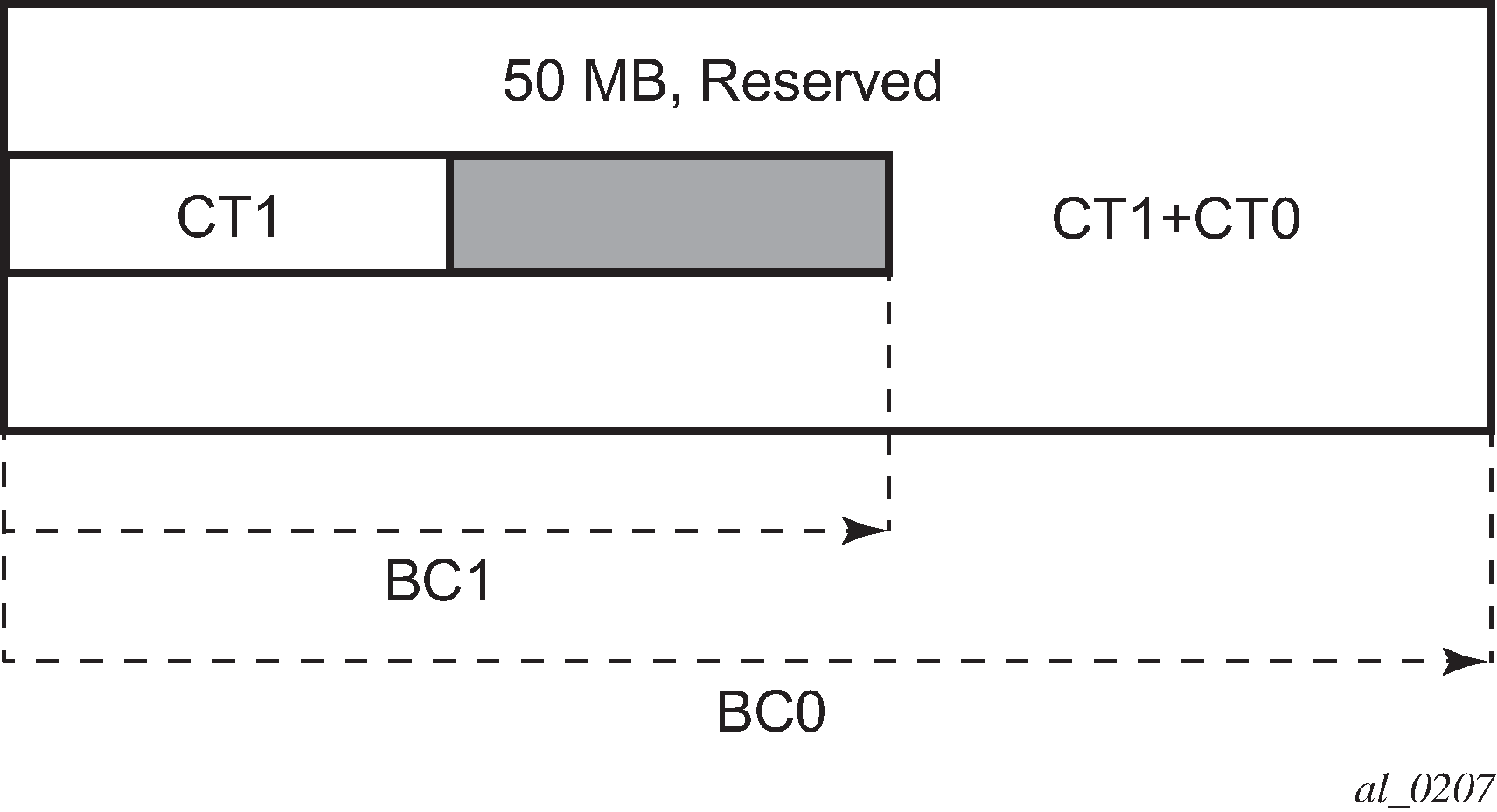
According to the RDM admission control policy:
Reserved (CT1, 0) = 50 ≤ 100 Mb/s
Reserved (CT0, 0) + Reserved (CT1, 0) = 50 ≤ 200 Mb/s
This results in the following unreserved bandwidth calculation.
Unreserved (CT1, 0) = BC1 – Reserved (CT1, 0) = 100 – 50 = 50 Mb/s
Unreserved (CT0, 0) = BC0 – Reserved (CT0, 0) – Reserved (CT1, 0) = 200 – 0 – 50= 150 Mb/s.
The bandwidth reserved by a doll is not available to itself or any of the outer dolls.
Suppose now another LSP comes with CT0, setup and holding priorities of 0 and a bandwidth 120 Mb/s.

Reserved (CT0, 0) = 120 ≤ 150 Mb/s
Reserved (CT0, 0) + Reserved (CT1, 0) = 120 + 50 = 170 ≤ 200 Mb/s
Unreserved (CT0, 0) = 150 -120 = 30 Mb/s
If we simply checked BC1, the formula would yield the wrong results:
Unreserved (CT1, 0) = BC1 – Reserved (CT1, 0) = 100 -50 = 50 Mb/s
Because of the encroaching of CT0 into CT1, we would need to deduct the overlapping reservation. This would then yield:
Unreserved (CT1, 0) = BC0 – Reserved (CT0, 0) – Reserved (CT1, 0) = 200 – 120 - 50 = 30 Mb/s, which is the correct figure.
Extending the formula with both equations:
Unreserved (CT1, 0) = Min [BC1 – Reserved (CT1, 0), BC0 – Reserved (CT0, 0) – Reserved (CT1, 0)] = Min [100 – 50, 200 – 120 – 50] = 30 Mb/s
An outer doll can encroach into an inner doll, reducing the bandwidth available for inner dolls.